A Clock Morph (The Cuis-Smalltalk Book)

Next: Back to Spacewar! Morphs, Previous: Going Vector, Up: The Fundamentals of Morph [Contents][Index]

7.2 A Clock Morph ¶

With all the things we have already learned, we can build a more sophisticated morph. Let’s build a ClockMorph as see in Figure 7.5.

Figure 7.5: A clock morph

Let’s create ClockMorph, the dial clock :

PlacedMorph subclass: #ClockMorph
   instanceVariableNames: ''
   classVariableNames: ''
   poolDictionaries: ''
   category: 'Morphic-Learning'

...and its drawing method in the category drawing:

ClockMorph>>drawOn: aCanvas
   aCanvas
      ellipseCenter: 0@0
      radius: 100
      borderWidth: 10
      borderColor: Color lightCyan
      fillColor: Color veryVeryLightGray.
   aCanvas drawString: 'XII' at: -13 @ -90 font: nil color: Color brown.
   aCanvas drawString: 'III' at: 66 @ -10 font: nil color: Color brown.
   aCanvas drawString: 'VI' at: -11 @ 70 font: nil color: Color brown.
   aCanvas drawString: 'IX' at: -90 @ -10 font: nil color: Color brown

Example 7.2: Drawing the clock dial

We create ClockHourHandMorph, the hand for the hours:

PlacedMorph subclass: #ClockHourHandMorph
   instanceVariableNames: ''
   classVariableNames: ''
   poolDictionaries: ''
   category: 'Morphic-Learning'

...and its drawing method in the category drawing:

ClockHourHandMorph>>drawOn: aCanvas
   aCanvas fillColor: (Color black alpha: 0.6) do: [
      aCanvas
         moveTo: 0 @ 10;
         lineTo: -5 @ 0;
         lineTo: 0 @ -50;
         lineTo: 5 @ 0;
         lineTo: 0 @ 10 ].

You can start playing with them. We could use several instances of a single ClockHandMorph, or create several classes. Here we chose to do the latter. Note that all the drawOn: methods use hardcoded constants for all coordinates. As we have seen before, this is not a limitation. We don’t need to write a lot of specialized trigonometric and scaling formulas to build Morphs in Cuis-Smalltalk!

By now, you might imagine what we are doing with all this, but please bear with us while we finish building our clock.

We create ClockMinuteHandMorph, the hand for the minutes:

PlacedMorph subclass: #ClockMinuteHandMorph
   instanceVariableNames: ''
   classVariableNames: ''
   poolDictionaries: ''
   category: 'Morphic-Learning'

...and its drawing method in the category drawing:

ClockMinuteHandMorph>>drawOn: aCanvas
   aCanvas fillColor: ((Color black) alpha: 0.6) do: [
      aCanvas
         moveTo: 0 @ 8;
         lineTo: -4 @ 0;
         lineTo: 0 @ -82;
         lineTo: 4 @ 0;
         lineTo: 0 @ 8 ]

And finally, the ClockSecondHandMorph, the hand for the seconds:

PlacedMorph subclass: #ClockSecondHandMorph
   instanceVariableNames: ''
   classVariableNames: ''
   poolDictionaries: ''
   category: 'Morphic-Learning'

...and its drawing method in the category drawing:

ClockSecondHandMorph>>drawOn: aCanvas
   aCanvas strokeWidth: 2.5 color: Color red do: [
      aCanvas
         moveTo: 0 @ 0;
         lineTo: 0 @ -85 ]

Now, all that is needed is to put our clock parts together in ClockMorph. In its method category initialization add its initialize method (accept the new names as instance variables):

ClockMorph>>initialize
   super initialize.
   self addMorph: (hourHand := ClockHourHandMorph new).
   self addMorph: (minuteHand := ClockMinuteHandMorph new).
   self addMorph: (secondHand := ClockSecondHandMorph new)

If you have not already added instance variables for the clock hands, the Cuis IDE will note this and ask what you want to do about it. We want to declare the three missing names as instance variables.

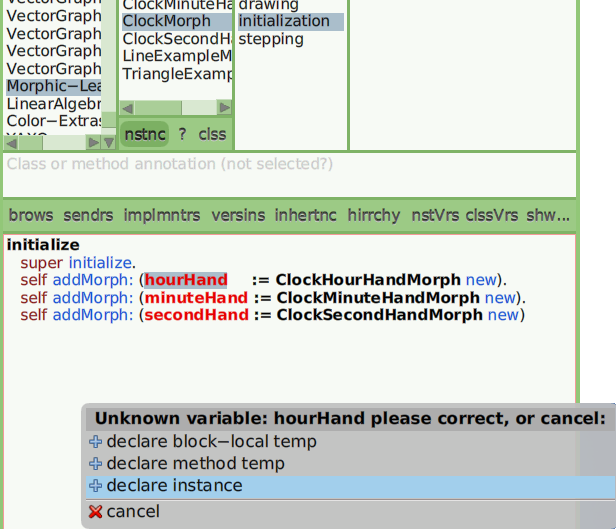
Figure 7.6: Declaring unknown variables as instance variables in current class

Your ClockMorph class definition should now be complete!

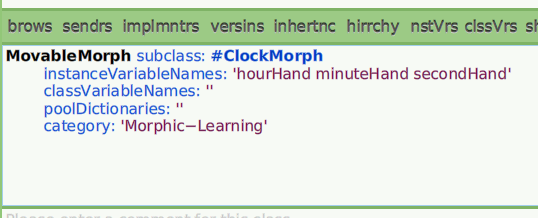
Figure 7.7: ClockMorph with instance variables added

Finally, we animate our clock. In method category stepping add the method:

ClockMorph>>wantsSteps
   ^ true

...and:

ClockMorph>>step
   | time |
   time := Time now.
   hourHand rotationDegrees: time hour * 30.
   minuteHand rotationDegrees: time minute * 6.
   secondHand rotationDegrees: time second * 6

Take a look at how we update the clock hands.

As we said before, any PlacedMorph defines a coordinate system for its own drawOn: method and also for its submorphs. This new coordinate system might include rotation or reflexion of the axis, and scaling of sizes, but by default they don’t. This means that they just translate the origin, by specifying where in the owner point 0 @ 0 is to be located.

The World coordinate system has 0 @ 0 at the top left corner, with X coordinates increasing to the right, and Y coordinates increasing downwards. Positive rotations go clockwise. This is the usual convention in graphics frameworks. Note that this is different from the usual mathematics convention, where Y increases upwards, and positive angles go counterclockwise.

So, how do we update the hands? For example, for the hour hand, one hour means 30 degrees, as 12 hours means 360 degrees or a whole turn. So, we multiply hours by 30 to get degrees. Minute and second hand work in a similar way, but as there are 60 minutes in one hour, and 60 seconds in one minute, we need to multiply them by 6 to get degrees. As rotation is done around the origin, and the clock has set the origin at its center (Example 7.2), there’s no need to set the position of the hands. Their 0 @ 0 origin will therefore be at the clock 0 @ 0, i.e. the center of the clock.

Figure 7.8: A fancy clock morph

Look at the clock on Figure 7.8. Don’t you think its hand for the seconds decorated with a red and yellow disc is fancy? How will you modify our clock morph to get this result?

Exercise 7.3: A fancy clock

Create some instances of your clock: ClockMorph new openInWorld. You can rotate and zoom. Look at the visual quality of the Roman numerals in the clock face, especially when rotated and zoomed. You don’t get this graphics quality on your regular programming environment! You can also extract the parts, or scale each separately. Another fun experiment is to extract the Roman numerals into a separate ClockFaceMorph, and make it submorph of the Clock. Then, you can rotate just the face, not the clock, and the clock will show fake time. Try it!

You might have noted two things that seem missing, though: How to compute bounding rectangles for Morphs, and how to detect if a Morph is being hit by the Hand, so you can move it or get a halo. The display rectangle that fully contains a morph is required by the framework to manage the required refresh of Display areas as a result of any change. But you don’t need to know this rectangle in order to build your own Morphs. In Cuis-Smalltalk, the framework computes it as needed, and stores it in the privateDisplayBounds variable. You don’t need to worry about that variable at all.

With respect to detecting if a Morph is being touched by the Hand, or more generally, if some pixel belongs to a Morph, truth is that during the drawing operation of a Morph, the framework indeed knows all the pixels it is affecting. The drawOn: method completely specifies the shape of the Morph. Therefore, there is no need to ask the programmer to code the Morph geometry again in a separate method! All that is needed is careful design of the framework itself, to avoid requiring programmers to handle this extra complexity.

The ideas we have outlined in this chapter are the fundamental ones in Morphic, and the framework is implemented in order to support them. Morphs (i.e. interactive graphic objects) are very general and flexible. They are not restricted to a conventional widget library, although such a library (rooted in BoxedMorph) is included and used for building all the Smalltalk tools.

The examples we have explored use the VectorGraphics framework. It includes VectorCanvas and HybridCanvas classes. Cuis-Smalltalk also includes the legacy BitBltCanvas class inherited from Squeak. BitBltCanvas doesn’t support the vector graphics drawing operations and doesn’t do anti-aliasing or zooming. But it is mature, and it relies on the BitBlt operation that is included in the VM. This means that it offers excellent performance.

To further explore Cuis-Smalltalk’ Morphic, evaluate Feature require: 'SVG', and then SVGMainMorph exampleLion openInWorld and the other examples there. Also, be sure to try the examples in the class category Morphic-Examples, among them execute Sample10PythagorasTree new openInWorld and play with the mouse wheel’s up and down, left and right directions.

Before we leave this section, here is a two lines change to turn our Cuis quartz clock²⁴ to an automatic Swiss clock²⁵ ²⁶:

ClockMorph>>stepTime
    ^ 100 "milliseconds"
ClockMorph>>step
../..
   secondHand rotationDegrees: (time second + (time nanoSecond * 1.0e-9))* 6

Try to understand how these changes affect the behavior of the seconds’ hand and at which fraction of a second it is rotating.

7.2 A Clock Morph ¶

Footnotes

(24)

(25)

(26)