7.3.1 Central star ¶

Our central star has an extent of 30 @ 30 we need to use in several places in the code. Therefore it makes sense to define a dedicated method to answer this value:

CentralStar>>morphExtent
   ^ `30 @ 30`

  An expression surrounded with backticks '`' is evaluated only once, when the method is first saved and compiled. This creates a compound literal value and improves the performance of the method since the expression is not evaluated each time the method is called: the pre-built value is used instead.

As you learnt previously, a morph draws itself from its drawOn: method. We draw the star as an ellipse with randomly fluctuating x and y radius:

CentralStar>>drawOn: canvas
   | radius |
   radius := self morphExtent // 2.
   canvas ellipseCenter: 0 @ 0
      radius: (radius x + (2 atRandom - 1)) @ (radius y + (2 atRandom - 1))
      borderWidth: 3 
      borderColor: Color orange 
      fillColor: Color yellow

The star diameters in the x and y directions are fluctuating independently of 0 to 2 units. The star does not look perfectly round.

Figure 7.9: A star with a fluctuating size

7.3.2 Space ship ¶

At the game start-up, the nose of the space ship is pointing to the top of the screen as seen in Figure 7.10 and the angle of its direction is therefore -90°, while the angle of its rotation is 0°. Remember the Y ordinate are oriented toward the bottom of the screen.

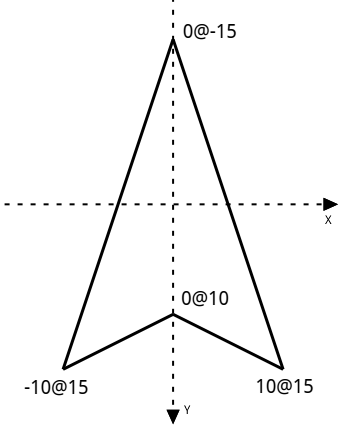
Figure 7.10: Space ship diagram at game start-up

Then its drawOn: method is written as:

SpaceShip>>drawOn: canvas
   | a b c d |
   a := 0 @ -15.
   b := -10 @ 15.
   c := 0 @ 10.
   d := 10 @ 15.
   canvas line: a to: b width: 2 color: color.
   canvas line: b to: c width: 2 color: color.
   canvas line: c to: d width: 2 color: color.
   canvas line: d to: a width: 2 color: color.
   "Draw gas exhaust"
   acceleration ifNotZero: [
      canvas line: c to: 0 @ 35 width: 1 color: Color gray]

When there is an acceleration from the engine, we draw a small gray line to represent the gas exhaust.

When the user turns the ship, the morph is rotated a bit by adjusting its heading:

SpaceShip>>right
"Rotate the ship to its right"
   self heading: self heading + 0.1

SpaceShip>>left
"Rotate the ship to its left"
   self heading: self heading - 0.1

But how does this heading affect the rotation of the morph?

Underneath, the MobileMorph is equipped with an affine transformation to scale, rotate and translate the coordinates passed as arguments to the drawing messages received by the canvas. Therefore, our heading methods are defined to match this internal representation and we use the rotation: method from the PlacedMorph class to rotate appropriately. The location attribute represents an affine transformation, and we get its rotation angle with the #radians message.

Mobile>>heading
   ^ location radians - Float halfPi
Mobile>>heading: aHeading
   self rotation: aHeading + Float halfPi

When a mobile is vertical, pointing to the top of the screen, its heading is -90° (-pi/2) in the screen coordinates system. In that situation the mobile is not rotated – or 0° rotated – therefore we add 90° (pi/2) to the heading to get the matching rotation angle of the mobile.

7.3.3 Torpedo ¶

Alike a space ship, when a torpedo is just instantiated its nose points in the direction of the top of the screen and its vertices are given by the Figure 7.11.

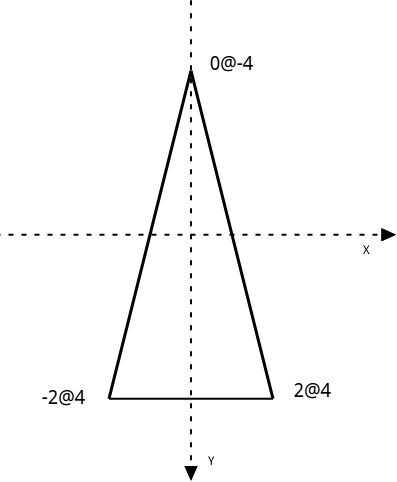
Figure 7.11: Torpedo diagram at game start-up

7.3.4 Drawing revisited ¶

As you may have observed, the SpaceShip and Torpedo drawOn: methods share the same logic: drawing a polygon given its vertices. We likely want to push this common logic to their common ancestor, the Mobile class. It needs to know about its vertices, so we may want to add an instance variable vertices initialized in its subclasses with an array containing the points:

PlacedMorph subclass: #Mobile
   instanceVariableNames: 'acceleration color velocity vertices'
   classVariableNames: ''
   poolDictionaries: ''
   category: 'Spacewar!'

SpaceShip>>initialize
   super initialize.
   vertices := {0@-15 . -10@15 . 0@10 . 10@15}.
   self resupply
   
Torpedo>>initialize
   super initialize.
   vertices := {0@-4 . -2@4 . 2@4}.
   lifeSpan := 500.
   acceleration := 3000

However this is not a good idea. Imagine the game play with 200 torpedoes, the vertices array will be duplicated 200 times with the same data!

Class instance variable ¶

In that kind of situation, what you want is a class instance variable defined in the class side – in contrast to the instance side where we have been coding until now.

We make use of the fact that all objects are instances of some class. The Mobile class is an instance of the class Class!

1. A class instance variable can be accessed and assigned only by the class itself in a class method.
2. An entity (i.e. a fired torpedo) can access class instance variables via class methods, by sending a message to a class (i.e. Torpedo) rather than to itself or some other entity.
3. In the class hierarchy, each subclass has its own instance of the class instance variable, and can assign a different value to it – in contrast with a class variable which is shared among all the subclasses (discussed later).
4. To edit the class instance variables and class methods, in the System Browser press the class button under the class list.

In the System Browser, we click the class button then we declare our variable in the Mobile class definition – Figure 7.12:

Mobile class
   instanceVariableNames: 'vertices'

Then we write an access method in the Mobile class, so SpaceShip and Torpedo instances can access it:

Mobile class>>vertices
   ^ vertices

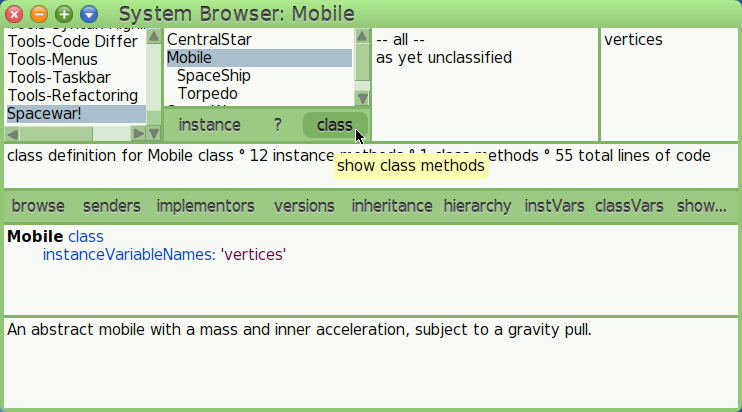
Figure 7.12: The class side of the System Browser

Next, each subclass is responsible to correctly initialize vertices with its initialize class method:

SpaceShip class>>initialize
"SpaceShip initialize"
   vertices :=  {0@-15 . -10@15 . 0@10 . 10@15}

Torpedo class>>initialize
"Torpedo initialize"
   vertices := {0@-4 . -2@4 . 2@4}

When a class is installed in Cuis-Smalltalk, its initialize class method is executed. Alternatively select the comment and execute it with Ctrl-d.

Experiment in a Workspace to understand how a class instance variable behaves:

SpaceShip vertices.
⇒ nil 
SpaceShip initialize.
SpaceShip vertices.
⇒ #(0@-15 -10@15 0@10 10@15) 

Torpedo vertices.
⇒ nil 
Torpedo initialize.
Torpedo vertices.
⇒ #(0@-4 -2@4 2@4)

This is really the behavior we want: SpaceShip and Torpedo instances have a different diagram. However, every instances of a SpaceShip will have the same diagram, referring to the same vertices array (i.e. same location in the computer memory).

Each instance asks its class side with the #class message:

aTorpedo class
⇒ Torpedo
self class
⇒ SpaceShip

The Torpedo’s drawOn: is rewritten to access the vertices in its class side:

Torpedo>>drawOn: canvas
   | vertices |
   vertices := self class vertices.
   canvas line: vertices first to: vertices second width: 2 color: color.
   canvas line: vertices third to: vertices second width: 2 color: color.
   canvas line: vertices first to: vertices third width: 2 color: color

So far, we still have this redundancy in the drawOn: methods. What we want is Mobile to be responsible to draw the polygon given a vertices array: self drawOn: canvas polygon: vertices.

The SpaceShip and Torpedo’s drawOn: will then be simply written as:

Torpedo>>drawOn: canvas
   self drawOn: canvas polygon: self class vertices

SpaceShip>>drawOn: canvas
   | vertices |
   vertices := self class vertices.
   self drawOn: canvas polygon: vertices.
   "Draw gas exhaust"
   acceleration ifNotZero: [
      canvas line: vertices third to: 0@35 width: 1 color: Color gray]

Class variable ¶

A class variable is written capitalized in the argument of classVariableNames: keyword:

PlacedMorph subclass: #Mobile
   instanceVariableNames: 'acceleration color velocity'
   classVariableNames: 'Vertices'
   poolDictionaries: ''
   category: 'Spacewar!'

As a class instance variable, it can be directly accessed from the class side and instances are granted access only with messages send to the class side. Contrary to a class instance variable, its value is common in the whole class hierarchy.

In Spacewar!, a class variable Vertices will have the same diagram for a space ship and a torpedo. This is not what we want.

SpaceShip>>vertices
   ^ `{0@-15 . -10@15 . 0@10 . 10@15}`

7.3.5 Drawing simplified ¶

Using a class variable in the present game design is a bit overkill. It was an excuse to present the concept of class variables. If the game came with an editor where the user redesigns the ship and torpedo diagrams, it would make sense to hold the vertices in a variable. But our vertices of the space ship and torpedo diagrams are constant. We do not modify them. As we did with the mass of the space ship – Example 3.16 – we can use a method returning a collection, surrounded with backtricks to improve efficiency.

SpaceShip>>vertices
   ^ `{0@-15 . -10@15 . 0@10 . 10@15}`
   
Torpedo>>vertices
   ^ `{0@-4 . -2@4 . 2@4}`

Then in the drawing methods, we replace self class vertices by self vertices.

7.3.6 Collisions revisited ¶

In Example 4.23, we have a very naive approach for collision between the central star and the ships, based on distance between morphs. It was very inaccurate.

In bitmap games, a classic way to deal with collision detection is to look at the intersections of the rectangles surrounding the graphic objects. The #displayBounds message sent to a morph answers its bounds in the display, a rectangle encompassing the morph given its rotation and scale.

Figure 7.13: The display bounds of a space ship

When browsing the Rectangle class, you learn the #intersects: message tells us if two rectangles overlap. This is what we need for a more accurate collision detection between the central star and the space ships:

SpaceWar>>collisionsShipsStar
   ships do: [:aShip | 
      (aShip displayBounds intersects: centralStar displayBounds) ifTrue: [
         aShip flashWith: Color red.
         self teleport: aShip]]

Nevertheless we use the VectorGraphics framework, its knows about the shape of each morph it is rendering. It uses this knowledge for collision detection at the pixel precision. We rewrite our detection method simpler with the #collides: message:

SpaceWar>>collisionsShipsStar
   ships do: [:aShip | 
      (aShip collides: centralStar) ifTrue: [
         aShip flashWith: Color red.
         self teleport: aShip]]